第12回 問題4 正答率 40.7%
《時計まわり》
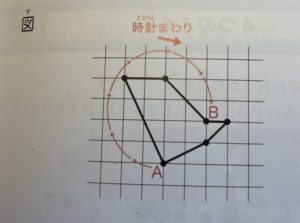
図のように、同じ大きさの正方形のマスの角を太い線でむすんで、
この形のまわりの長さは何cmですか。
【教え方】
図形の問題なので、それぞれの辺を記号で表していきます。
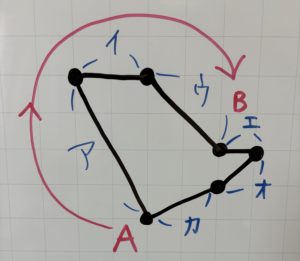
このとき同じような形はないか?と問い、
アとカ
イとエ
オとウ
それぞれが同じ形であることに注目して、
次に、記号を使った式を立てます。
ア=カ+カ もしくは、ア=カ×2
イ=エ+エ もしくは、イ=エ×2
ウ=オ+オ もしくは、ウ=オ×2
問題文より、AからBまではア+イ+ウなので、
ア+イ+ウ=20 ならば、エ+オ+カは、その半分の10cmです。
求められているのは、この形のまわりの長さなので
ア+イ+ウ+エ+オ+カ=20+10=30
【答え】
30cm



